SIMC 2020
Tất tần tật về 1 tuần mình thi SIMC

Blog này sẽ nói về 1 tuần mình tham gia SIMC và 1 tháng chuẩn bị trước đó. SIMC là cuộc thi toán ứng dụng được tổ chức 2 năm một lần bởi đại học NUS. Thông thường mỗi trường sẽ cử 3 học sinh sang Singapore để thi trực tiếp trong 3 ngày nhưng do Covid nên cuộc thi sẽ tổ chức online trong 1 tuần và mỗi đội sẽ gửi 1 video thuyết trình bài làm của mình. Trường mình năm nay cũng tham dự với thành viên là mình cũng 2 anh khóa trên.
Để chuẩn bị cho cuộc thi, trước đó 1 tháng trường mình có tập huấn 1 số buổi về toán ứng dụng cũng như các chủ để liên quan. Sau đó cả nhóm bắt đầu xem các đề năm trước và làm thử. (nếu rảnh mình sẽ viết blog riêng về các đề thi cũ nhưng blog này mình sẽ tập trung vào đề năm nay). Cuối cùng vào ngày 12 tháng 10, cuộc thi bắt đầu. Anh Nghĩa và anh Lâm (2 teammate của mình) sẽ tập trung vào phần ý tưởng còn mình đảm nhận nhiệm vụ trình bày và thuyết trình. Trong quá trình thi, ngoài những lúc làm ở nhà thì đội mình cũng thường đến trường hoặc nhà anh Lâm giải cũng nhau.
Chủ đề năm nay là bãi đỗ xe. Coi bãi đỗ xe là 1 bảng ô vuông còn ô tô là hình chữ nhật \(1\times2\). Nhiệm vụ của mình là thiết kế 1 bãi đỗ xe sao cho tất cả xe đều có thể ra vào được và có độ hiệu quả cao nhất (độ hiệu quả được tính bằng số xe chứa được chia cho diện tích bãi đỗ)
Ở câu hỏi đầu tiên, mình cần tối đa hóa độ hiệu quả của bãi đỗ xe \(N \times N\) với \(N\) rất lớn. Đội mình ra được đáp án là \(4/7\). Mình chia bãi đỗ thành các hình chữ nhật \(7\times N\) có các cạnh song song với cạnh của bãi đỗ. Cổng ra vào là đoạn thẳng AB sao cho \((AC=BD=2.5)\). Khi đó độ hiệu quả là $$[\frac{N}{7}]*(2N-4)*2/N^2\approx\frac{4}{7}$$ Ngoài ra mình cũng chứng minh được cận trên của độ hiệu quả là \(\frac{4}{5}\).
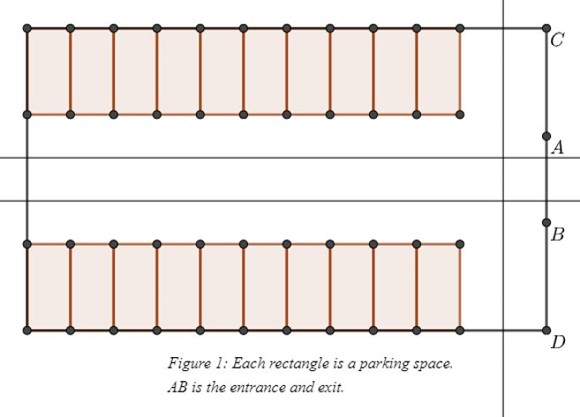
Câu 2 cũng tương tự với câu 1 nhưng lần này bãi đỗ xe có dạng là \(6 \times N\) và \(10\times N\). Mình cũng áp dụng thiết kế gần tương tự với câu 1 để đạt độ hiệu quả lần lượt \(7/15\) và \(12/25\).
Từ câu hỏi thứ 3, ô tô được biểu diễn bằng hình chữ nhật 1 × 2 có thể tiến, lùi và quay quanh \ một vòng tròn có bán kính 2 tính từ bánh sau của ô tô. Dưới đây là hình minh họa:
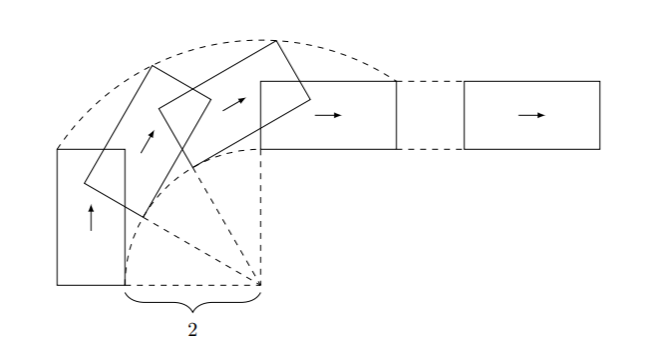
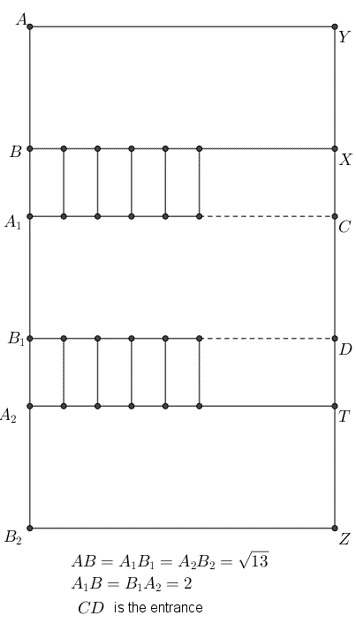
Khi đó độ hiệu quả là: $$2*\lfloor\frac{M-\sqrt{13}}{2+\sqrt{13}}\rfloor*(N-4)/(MN)\approx 0.36 $$
với \(M,N\) rất lớn biểu thức trên xấp xỉ bằng \(2/(2+\sqrt{13})\).
Câu 3b và 3c cũng tương tự nhưng ô tô giờ có thể đi lùi và xoay lùi xe. Khi đó độ hiệu quả xấp xỉ \(0.53\).
Câu hỏi cuối cùng, câu số 4, là 1 câu hỏi ứng dụng trong thực tế. Một trong những cách đã được áp dụng trong thực tế là xếp các xe theo hình chéo thay vì xếp thẳng. Điều này giúp ô tô dễ di chuyển ra vào chỗ đỗ hơn cũng như tiết kiệm diện tích. Ngoài ra còn có nhiều phương thức và công nghệ khác cũng được áp dụng nhằm tăng độ hiệu quả (phần này anh Lâm làm nên mình cũng không rõ lắm :<)
Tổng kết lại cuộc thi thì mặc dù thi liên tục trong 1 tuần có hơi mệt nhưng sau khi có được thành quả hoàn chỉnh thì mình cũng thấy khá vui và bõ công sức. Ngoài ra mình cũng có cơ hội được làm việc với 2 anh cực kì khủng (cả 2 anh đều nằm trong đội IMO 2020 và 2021).
Nếu thích các bạn có thể xem đề 2020 tại đây:
https://www.nushigh.edu.sg/qql/slot/u90/file/simc/SIMC2020ChallengeQuestion.pdf