Điểm nguyên
Giới thiệu về điểm nguyên và những định lí liên quan

- Giới thiệu
- Định lí Pick
- Chứng minh
- Hình vuông đơn vị: Xét hình vuông có cạnh bằng 1 đơn vị. Khi đó \(S=1,I=0,B=4\) (thỏa mãn công thức).
- Hình chữ nhật có cạnh song song trục tọa độ:
Đặt \(a\) và \(b\) là chiều dài cạnh hình chữ nhật. Khi đó, \(S=ab,I=(a-1)(b-1),B=2(a+b)\) (sau khi biến đổi đại số 1 chút ta cũng thấy thỏa mãn công thức).
-
Tam giác có 2 cạnh góc vuông song song với trục tọa độ:
Để chứng minh điều này, ta nhận thấy rằng mọi tam giác như vậy đều có thể tạo ra bằng cách cắt chéo hình chữ nhật có độ dài là chiều dài 2 cạnh góc vuông. Gọi tam giác là \(tri\) ,hình chữ nhật là \(rect\) còn số điểm nguyên thuộc cạnh huyền \(tri\) là \(c\) (không chứa 2 đầu mút). Khi đó: $$B_{rect}=2B_{tri}-2-2c$$ Để cho dễ hiểu hơn ta xét hình minh họa sau:
Đặt số điểm nguyên thuộc đoạn AB bất kì là \(P_{AB}\).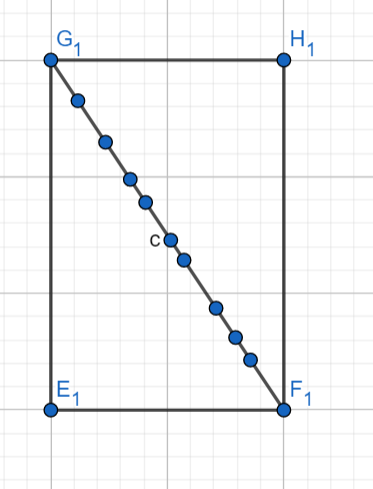
Ta có $$B_{tri}=B_{G_1E_1F_1} = P_{G_1E_1}+P_{E_1F_1}+P_{F_1G_1}-3 = P_{G_1E_1}+P_{E_1F_1}+c-1$$ (-3 do 3 điểm \(G_1,E_1,F_1\) được tính 2 lần) $$B_{rect} = P_{G_1E_1}+P_{E_1F_1}+P_{F_1H_1}+P_{H_1G_1}-4 = 2(P_{G_1E_1}+P_{E_1F_1})-4 = 2(B_{tri}-c+1)-4=2B_{tri}-2c-2 $$ Kế tiếp ta có: \(I_{rect}=2I_{tri}+c\) (do các điểm nguyên thuộc đường chéo không thuộc \(I_{tri}\) nên ta cộng thêm c) Bước cuối cùng chỉ là biến đổi đại số: $$S_{tri}=\frac{S_{rect}}{2}=\frac{I_{rect}+B_{rect}/2-1}{2}=\frac{2I_{tri}+c+B_{tri}-c-1-1}{2}=I_{tri}+\frac{B_{tri}}{2}-1$$ Vậy là ta có biểu thức cần tìm cũng như chứng minh rằng biểu thức đúng với mọi giá trị của \(c\). Từ đây ta cũng có 1 nhận xét là nếu đa giác A thỏa mãn biểu thức thì khi cắt A thành các đa giác nhỏ hơn, các đa giác đó cũng thỏa mãn. - Tam giác có 3 đỉnh nguyên
- Đa giác nguyên bất kì
1.1. Khái niệm
Điểm nguyên (Lattice point) là các điểm trong hệ tọa độ Descartes mà có tọa độ nguyên.
1.2. Ví dụ
Các điểm như \((1,3)\) hay \((-4,0)\) là các điểm nguyên trong không gian 2 chiều. Còn điểm \((10,-5,0)\) là 1 điểm nguyên trong không gian 3 chiều.
1.3. Một khái niệm khác
Người ta còn định nghĩa điểm nguyên là giao điểm của 2 hoặc nhiều đường đơn vị (đường thẳng song song với 1 trục tọa độ và đi qua 1 điểm đơn vị). Các đường đơn vị ấy được gọi là mạng điểm (point lattice). Chính vì điều này nên điểm nguyên cũng được gọi là điểm mạng. Trong một mặt phẳng, các điểm nguyên có thể được xây dựng bằng các ô đơn vị có dạng hình vuông, hình chữ nhật, và các hình dạng khác nhưng phổ biến nhất là hình vuông.
1.4. Bài tập ví dụ
Một mạng điểm được dựng bằng thêm tất cả các điểm \((a,b)\) sao cho \(a\) và \(b\) là các số nguyên dương. Tìm các điểm thuộc mạng điểm nằm trên đường thẳng \(y=-3x+8\).
Giải: Có \(y>0 \Rightarrow -3x+8>0 \Rightarrow x \leq 2\). Do đó, \((1,5)\) và \((2,2)\) là 2 điểm thỏa mãn.
Một đa giác không tự cắt chính nó và có các đỉnh là điểm nguyên được gọi là đa giác nguyên (Lattice polygon). Định lý Pick giúp ta tính diện tích đa giác này sử dụng số đỉnh nằm trên biên và số đỉnh nằm bên trong đa giác.
2.1. Công thức
Đặt diện tích của đa giác nguyên là \(S(S>0)\), số điểm nguyên nằm trong đa giác (không tính nằm trên biên) là \(I\) và số điểm nguyên nằm trên biên là \(B\). Khi đó: $$S=I+\frac{B}{2}-1$$ Nói cách khác, nếu ta biết giá trị \(I, B\) thì ta có thể tính \(S\) trong \(O(1)\) mà không cần biết tạo độ các đỉnh. Công thức này được phát hiện và chứng minh bới nhà toán học Áo Georg Alexander Pick vào năm 1899.
Ta chứng minh từ các đa giác đơn giản đến phức tạp:
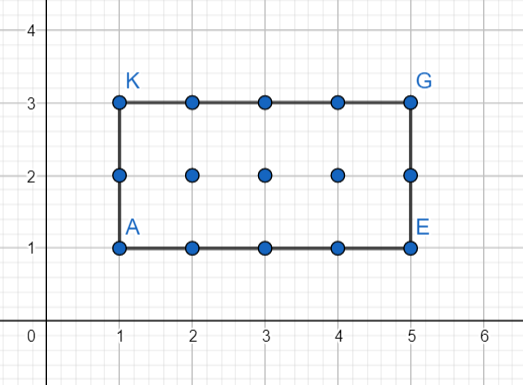
Lưu ý rằng bất kỳ hình tam giác nào như vậy đều có thể được biến thành hình chữ nhật bằng cách gắn các hình tam giác có cạnh góc vuông song song với trục (cần gắn tối đa 3 hình tam giác). Chứng minh tương tự trên, ta có được công thức cho bất kỳ tam giác có 3 đỉnh nguyên nào.
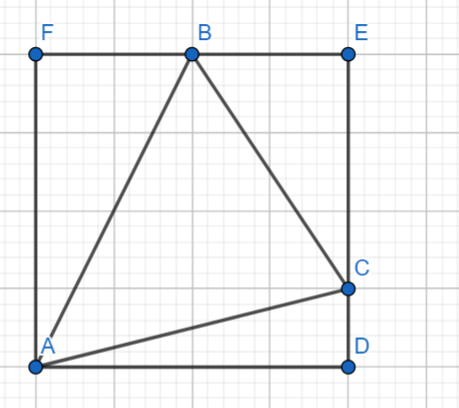
Ta chia đa giác \(n\) đỉnh \(A_1A_2...A_n\) thành \(n-2\) tam giác có 3 đỉnh nguyên \(A_1A_2A_3,A_1A_3A_4,...,A_1A_{n-1}A_{n}\) rồi áp dụng biểu thức là xong.